Before you understand what is Transversal, you must know:
What are Lines ?
What are Intersecting Lines ?
What is Intersection Point ?
Definition: A line which intersect two or more lines at different points is known as a Transversal
E.g. In the following diagram:
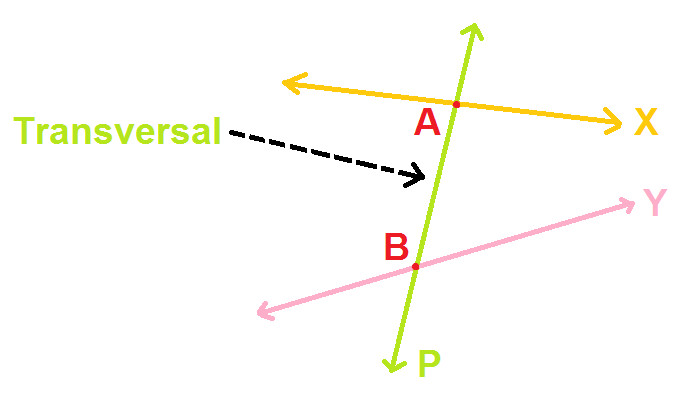
Lines X and Y are intersected by another Line P at points A and B respectively.
Or we can also say that:
Line P intersects two Lines X and Y at different points i.e. A and B respectively.
Hence, Line P is transversal to Lines X and Y.
Now, in the following diagram:
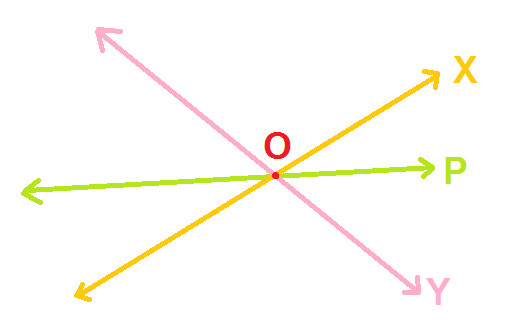
You can see that here also, Line P is intersecting Lines X and Y.
So, Can we say here also that Line P is transversal to Lines X and Y ?
No, Line P is not a transversal to Lines X and Y because it does not intersect Lines X and Y at different points.
|






