Total Surface Area of Right Circular Cone

Total Surface Area of Cone

Lateral Surface Area of Cone

Volume of Cone

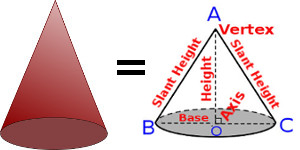
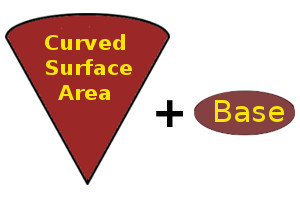
What is total surface area of right circular cone ? Suppose we have cone shape object like as mentioned in the below diagram If we cut open it from the slant height the shape of cone will be as mentioned in the following diagram so, total surface area of of cone is : Base Area (radius of cone) + Curved surface area Formula of Curved Surface Area is : Π x Radius x Slant Height Formula of Base Area is : Π x Radius2 or T.S.A. = Base Area + Curved surface area Or T.S.A. of cone = Π x Radius2 + ( Π x Radius x Slant Height ) Or T.S.A. of cone = Π x R2 + ( Π x R x SH ) Or T.S.A. of cone = Π x R (R + SH) Let's try out some examples to find total surface area of right circular cone Example 1: Find total surface area of cone which has a radius of of 3m and slant height of 5m Solution: Given things are Radius = 3m Slant Height = 4m As we know that total surface area of cone = Π x R (R + SH) we get T.S.A. of cone = Π x R (R + SH) value of Π : 3.142 T.S.A. of cone = 3.142 X 3 (3 + 5) T.S.A. of cone = 3.142 X 3 (8) T.S.A. of cone = 9.426 X 8 T.S.A. of cone = 75.408m Example 2: Find the slant height and total surface area of cone which has a radius of of 3m and height of 4m Solution : The given things are Radius = 3m Height = 4m Slant Height = ? First we will find the slant height of cone by using the Pythagoras theorem and we get Slant height2 = height2 + radius2 S.H.2 = (4)2 + (3)2 S.H.2 = 16 + 9 S.H.2 = 25 S.H. = √ 25 S.H. = 5m As we now know the slant height i.e. 5m we can now apply the formula of total surface area of cone As total surface area of cone = Π x R (R + SH) we get T.S.A. of cone = Π x R (R + SH) value of Π : 3.142 T.S.A. of cone = 3.142 X 3 (3 + 5) T.S.A. of cone = 3.142 X 3 (8) T.S.A. of cone = 9.426 X 8 T.S.A. of cone = 75.408m Example 3: Find the height and total surface area of cone which has a radius of of 6m and slant height of 10m Solution : The given things are Radius = 6m Height = ? Slant Height = 10m First we will find the height of cone by using the Pythagoras theorem and we get Slant height2 = height2 + radius2 102 = (Height)2 + (6)2 100 = (Height)2 + 36 (Height)2 = 100 - 36 (Height)2 = 64 Height = √ 64 Height = 8m Now we will apply the formula of total surface area of cone As total surface area of cone = Π x R (R + SH) we get T.S.A. of cone = Π x R (R + SH) value of Π : 3.142 T.S.A. of cone = 3.142 X 6 (6 + 10) T.S.A. of cone = 3.142 X 6 (16) T.S.A. of cone = 18.852 X 16 T.S.A. of cone = 301.632m Example 4: Find the total surface area of cone which has a height of 12m and a slant height of 15m Solution : The given things are Radius = ? Height = 12m Slant Height = 15m First we will find the radius of cone by using the Pythagoras theorem and we get Slant height2 = height2 + radius2 152 = (12)2 + radius2 152 = 144 + radius2 225 = 144 + radius2 radius2 = 225 - 144 radius2 = 81 radius = √ 81 radius = 9 Now we will apply the formula of total surface area of cone As total surface area of cone = Π x R (R + SH) we get T.S.A. of cone = Π x R (R + SH) value of Π : 3.142 T.S.A. of cone = 3.142 X 9 (9 + 15) T.S.A. of cone = 3.142 X 9 (24) T.S.A. of cone = 28.278 X 24 T.S.A. of cone = 678.672m Example : 5 - Find curved surface area of cone which has a radius of 3m and height of 4m Solution : First we will find the slant height of cone by using the Pythagoras theorem and we get Slant height2 = height2 + radius2 S.H.2 = (4)2 + (3)2 S.H.2 = 16 + 9 S.H.2 = 25 S.H. = √ 25 S.H. = 5m Now we will find curved surface area C.S.A. = Π x Radius x Slant Height C.S.A. = 3.142 X 3 X 5 C.S.A. = 47.13m2