Before you study this topic; you are adviced to study
Define Right Angled Triangle
Define Congruence / Congruent
Congruent Triangles
Corresponding Parts of Congruent Triangles
RHS rule Congruence of right angled triangle illustrates that, if hypotenuse and one side of right angled triangle are equal to the corresponding hypotenuse and one side of another right angled triangle; then both the right angled triangle are said to be congruent.
Example: Following are two diagrams of triangle with few of its measurements:

Is △ ABC ≅ △ PQR
Solution: As shown in the given diagrams:
△ ABC is a right angled triangle at ∠ B
△ PQR is a right angled triangle at ∠ Q
Also, we have:
∠ B = ∠ Q (90° each)
BC = QR (3 cm)
AC = PR (6 cm)
Therefore, RHS congruence rules apply here and we get the following corresponding relationships:
A ↔ P
B ↔ Q
C ↔ R
Hence, △ ABC ≅ △ PQR
Justification / Proof - RHS Congruence Rule
Now, let's justify or proof of RHS Rule of Congruence with the help of following three checks:
Check 1:
There is a given right angled triangle XYZ right angled at X and length of one side XY is 5cm. You are asked to construct a triangle ABC (right angled at B) congruent to triangle XYZ.
Can you do that ??
With length of one side is given i.e. 5cm, following right angled triangles can be formed:
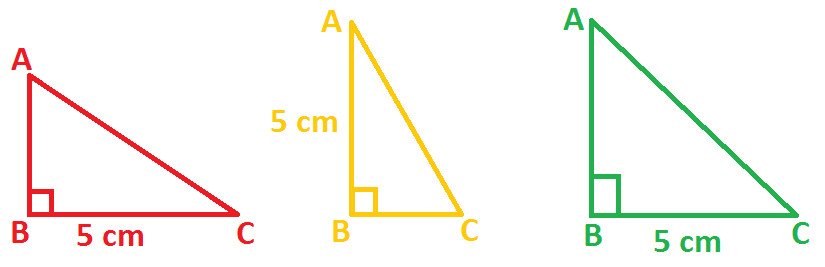
From the above diagram of triangles, you can observe that given triangle XYZ can be any of the following, or in other words we can say that we are not sure which diagram of triangle ABC is congruent to Triangle XYZ.
Hence, this confirms that two triangles cannot be congruent, if one side of a right angled triangle is equal to the corresponding one side of another right angled triangle.
Check 2:
There is a given right angled triangle XYZ right angled at X and length of hypotenuse YZ is 7 cm. You are asked to construct a triangle ABC (right angled at B) congruent to triangle XYZ.
Can you do that ??
With length of hypotenuse is given i.e. 7 cm, following right angled triangles can be formed:

From the above diagram of triangles, you can observe that given triangle XYZ can be any of the following, or in other words we can say that we are not sure which diagram of triangle ABC is congruent to Triangle XYZ.
Hence, this confirms that two triangles cannot be congruent, if hypotenuse of a right angled triangle is equal to the corresponding hypotenuse of another right angled triangle.
Check 3:
There is a given right angled triangle XYZ right angled at X and length of hypotenuse YZ is 7 cm and one side XY is 5 cm. You are asked to construct a triangle ABC (right angled at B) congruent to triangle XYZ.
Can you construct a triangle ABC congruent to triangle XYZ ?
Let's try to construct a triangle ABC congruent to triangle XYZ, when length of hypotenuse and one side are given.
Steps of construction are as follows:
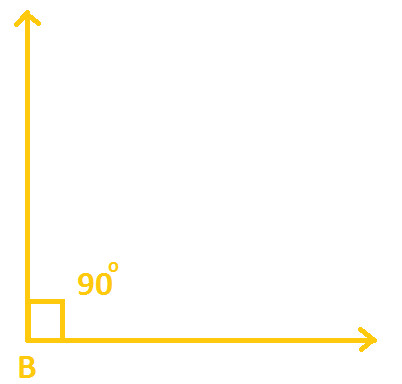
Step 1: With the help of a protractor, draw a right angle (with right angled at B), as shown in the below diagram:
Step 2: Now with compass 5 cm wide opened and with B as center; draw an arc of which cuts one of the arm of ∠ B; as shown below:
And label point as C, at which the arc cuts arms of ∠ B; as shown below:
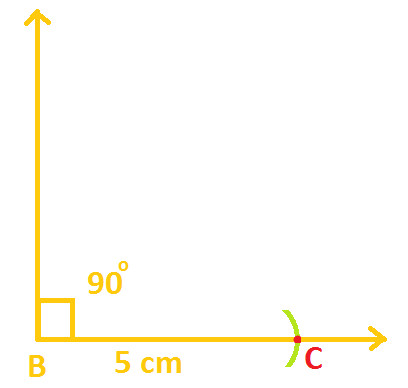
Therefore, we get BC = 5 cm, as shown above:
Step 3: Step 2: Now with compass 7 cm wide opened and with c as center; draw an arc of which cuts other arm of ∠ B; as shown below:
And label point as A, at which the arc cuts arms of ∠ B; as shown below:

Step 4: Join Points A and C and on checking with ruler you can observe that:
AC = 7 cm (as shown below):

Therefore resultant figure is a right angled triangle ABC with:
∠ B = 90°
BC = 5 cm
AC = 7 cm
Now you can see that:
BC ↔ XY (5 cm each)
AC ↔ ZY (7 cm each)
∠ B ↔ ∠ X (45° each)
So, on the basis above correspondence we get:
△ BCA ≅ △ XYZ
Hence, this proves RHS rule of Congruence which says:
If hypotenuse and one side of right angled triangle are equal to the corresponding hypotenuse and one side of another right angled triangle; then both the right angled triangle are said to be congruent.
Study More Solved Questions / Examples
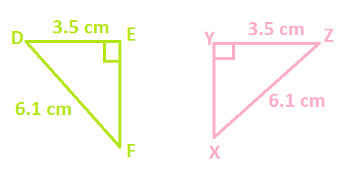
Below are two right angled triangles with measurements of few parts,
Prove △ DEF ≅ △ ZYX
 |
Following diagram represents Rectangle ABCD and AC = BD. Prove △ ABC ≅ △ DCB
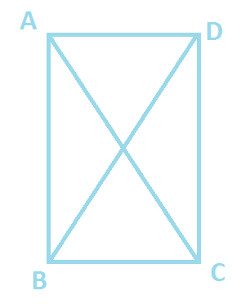 |
Observe the below diagram and Prove △ RPS ≅ △ QPS
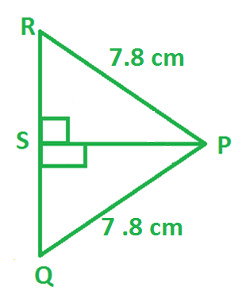 |
| | |






