Below diagram represent, construction of Perpendicular Bisector of a given Line Segment AB.
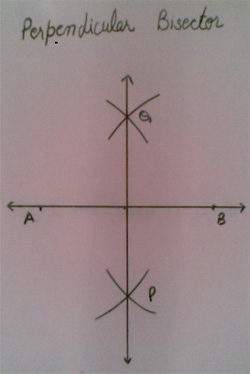
In the above diagram, Line Segment AB is given and its Perpendicular Bisector is done in the following steps
1.) With A as centre and radius more than half of AB, draw two arcs on upper and lower sides of Line segment AB
2.) With B as centre and same radius, draw another two arcs on upper and lower sides of Line segment AB, which cuts previous arcs at P and Q.
3.) Join P and Q
Therefore, PQ is Perpendicular Bisector of Line Segment AB.
|






