Before you understand this topic, you are advised to read:
What is Parallelogram ?
What are Parallel Lines ?
What are Congruent figures ?
What are the rules of Congruent Triangle ?
What are Transversal Lines ?
What are Corresponding Angles ?
What is Angle Sum Property of Triangle ?
This is one of the properties of parallelogram which says parallelograms on the same base and between same parallel lines are equal in area
Let's first understand how this situation looks like:
Observe the following diagram:
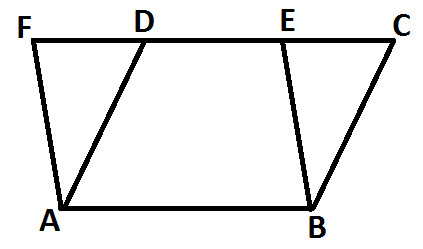
In the above diagram; AB is parallel to FC, AD is parallel to BC and AF is parallel to BE (as highlighted below):
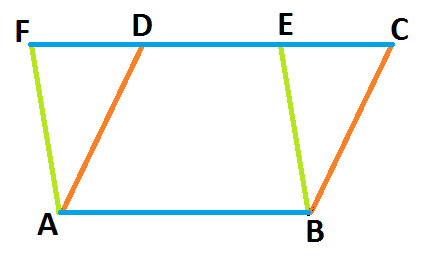
Observe carefully and you can notice that in the above diagram there are two parallelograms (as shown below)
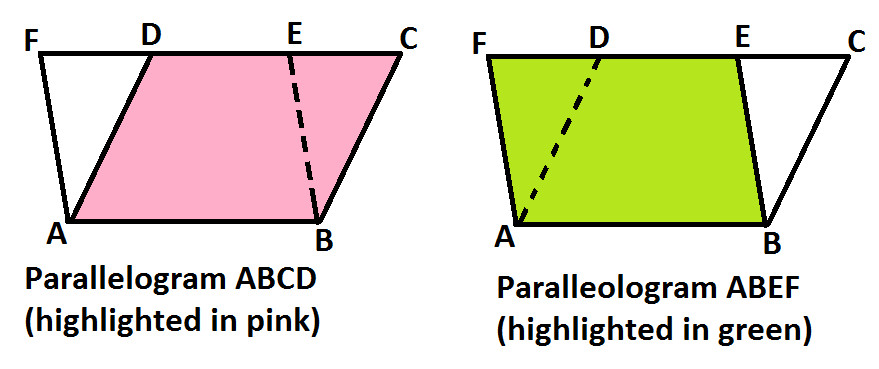
Also, you can notice that both the parallelograms ABCD and ABEF are on the same base i.e. AB (as shown below)
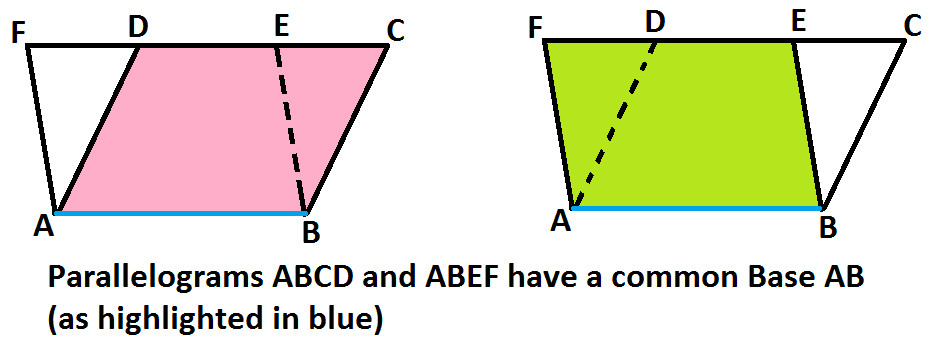
And both the parallelograms ABCD and ABEF are between same parallel lines AB and FC (as shown below)
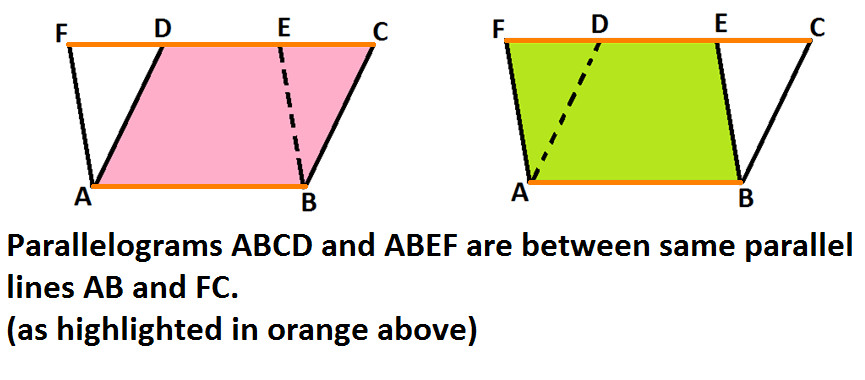
Hence, you can see how parallelograms can be on same base and between same parallel lines.
Now, let's prove this property that areas of parallelograms on the same base and between same parallel lines are same.
Observe the following diagram:

Take two triangles i.e. △ ADF & △ BEC. And mark few angles (as shown below):
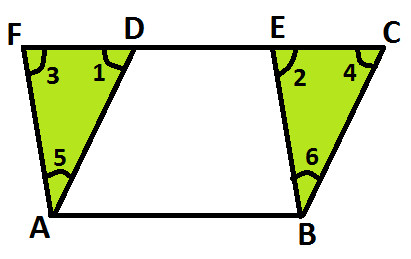
Now, in two triangles, △ ADF and △ BEC:
∠ 1 = ∠ 4 (Corresponding angles, AD // BC and FC is a transversal) ..... (Statement 1)
AF = BE (Opposite sides of parallelogram ABEF are equal) ..... (Statement 2)
∠ 3 = ∠ 2 (Corresponding angles, AF // BE and FC is a transversal) ..... (Statement 3)
From statement 1 and statement 3, we get:
∠ 5 = ∠ 6 (Angle sum property) ..... (statement 4)
From statement 2, 3 and 4; By ASA rule of congruency, its' proved that:
△ ADF ≅ △ BEC
Since, we know that areas of congruent figures are equal; we get:
Area of △ ADF = Area of △ BEC
Add area of quadrilateral ABED on both sides and we get:
Area of △ ADF + Area of quadrilateral ABED = Area of △ BEC + Area of quadrilateral ABED
Area of △ ADF + Area of quadrilateral ABED = Parallelogram ABEF
Showing this with the help of following diagram:
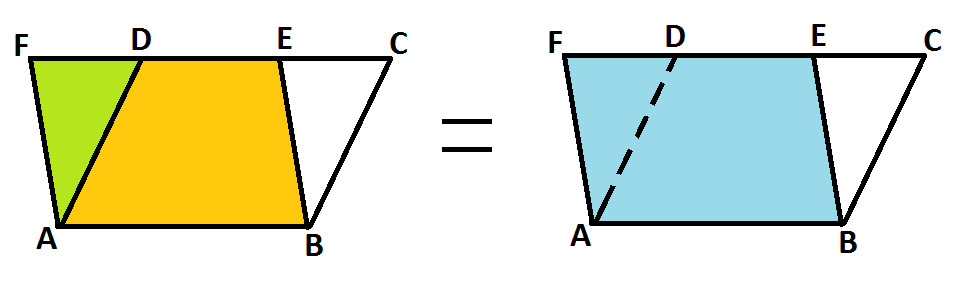
Area of △ BEC + Area of quadrilateral ABED = Parallelogram ABCD
Showing this with the help of following diagram:
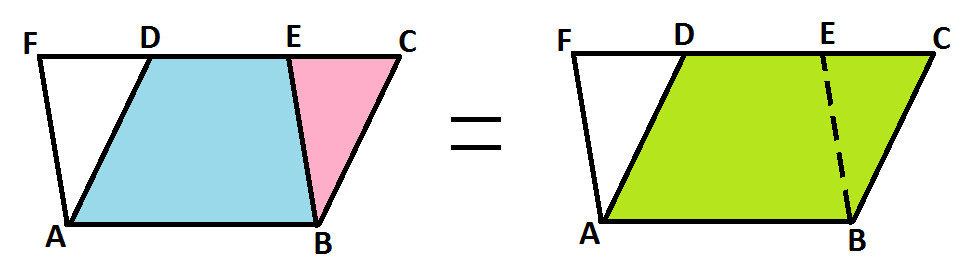
So apply the values and we get:
Parallelogram ABEF = Parallelogram ABCD
Hence, this proves the property parallelograms on the same base and between same parallel lines are equal in areas.
Now the converse of this property also stands true:
Parallelograms on the same base and having equal areas lies between the same parallel lines
|






