What is Mid-Point Property of Triangle ?
Mid point property of triangle says : The line segment joining the mid-points of two sides of a triangle, is parallel to the third side
Let's understand this with the help of following diagram:

ABC is a triangle
X and Y are the mid points of sides AC and BC respectively
XY is the line segment which joins the mid-points of AC and BC sides
Now, Mid point property of triangle says that the line segment joining the mid-points of two sides of a triangle, is parallel to the third side. So in context of the above diagram, we get:
XY // AB
How to prove the mid-point property of triangle:
Before you understand how to prove this property, you are advised to read:
What is Transversal ?
What are Alternative Interior Angles of Transversal ?
What are Vertically Opposite Angles ?
What is Congruent Triangle ?
What are the Rules of Congruency ?
Observe the below diagram:

ABC is a triangle
X and Y are the mid points of sides AC and BC respectively, so we get:
AX = XC and CY = YB ..... (statement 1)
Now, from vertex B draw a line BL parallel to AC (as shown below)
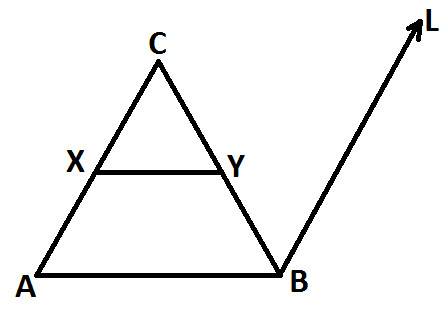
Extend line XY such that it meets BL at Z (as shown below):
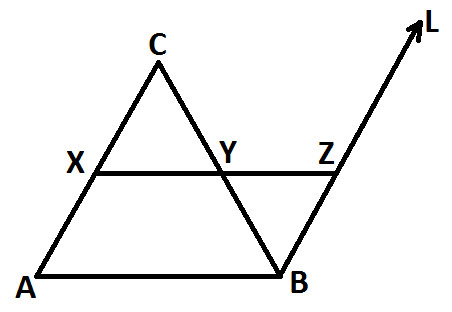
Now, BL // AC, so we can also say that:
AX // BZ ..... (statement 2)
Take two Triangles XYC and YZB (as highlighted in below diagram):
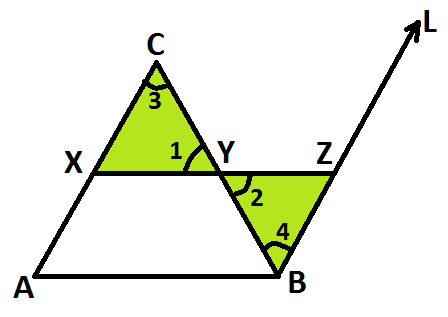
In △ CXY and △ YZB
∠ 1 = ∠ 2 (vertically opposite angles)
CY = YB (proved in statement 1)
∠ 3 = ∠ 4 (Alternative interior angles - AC // BL, CB is a transversal)
Therefore, by ASA rule of Congruency, we get:
△ CXY ≅ △ YZB
Since, △ CXY ≅ △ YZB, so we get:
XC = BZ (because corresponding sides of congruent triangles are equal) ..... (Statement 3)
From statement 1:
AX = XC
From statement 3:
XC = BZ
So, from statement 1 and 3, we get:
AX = BZ ..... (statement 4)
Now, observe Quadrilateral ABZX (as highlighted in below diagram):
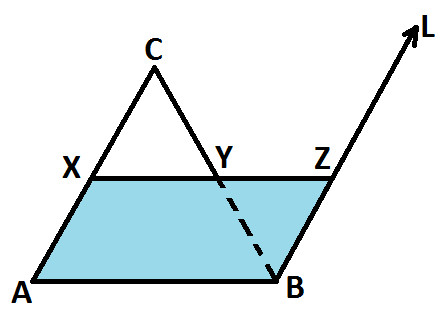
From statement 2 and 4, we get:
AX // BZ
AX = BZ
Since AX and BZ are opposite side, so we get:
Quadrilateral ABZX is a parallelogram (because if opposite side of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram)
Now, in parallelogram ABZX, we get:
XZ // AB (because in parallelogram opposite side are parallel)
Or we can also write it as:
XY // AB
Hence proved, Mid point property of triangle : The line segment joining the mid-points of two sides of a triangle, is parallel to the third side
Now, since Mid point property is proved, so we get converse of this property i.e.:
The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
|






