Before you study exterior angle property of a triangle, you are advised to read:
What are Interior Angles of a Triangle ?
What are Exterior Angles of a Triangle
What are Interior Opposite Angles ?
Exterior Angle Property of a Triangle states that measure of exterior angle of a triangle is equals to the sum of measures of its interior opposite angles.
In order words:
Exterior Angle = Sum of Interior Opposite Angles
As shown in the following diagram:
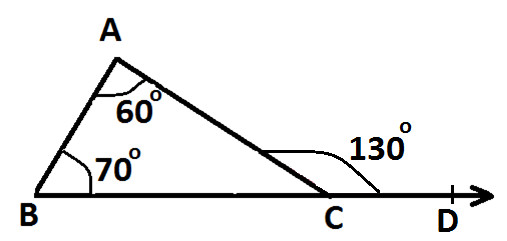
Exterior Angle is ∠ ACD and its two interior opposite angles are ∠ BAC and ∠ ABC
Measure of ∠ ACD = 130°
Measure of one interior ∠ BAC = 60°
Measure of other interior ∠ ABC = 70°
Now, we can observe that:
130° = 60° + 70°
Or we can say:
∠ ACD = ∠ BAC and ∠ ABC
Hence, its demonstrated that measure of exterior angle of a triangle is equals to the sum of measures of its interior opposite angles
Now let's prove/justify External Angle Property of a Triangle:
Before we prove/justify this topic, you are advised to read:
What is Angle Sum Property of a Triangle ?
What is Linear Pair ?
External Angle Property of a Triangle is proved or justified as follows:
In the following diagram:
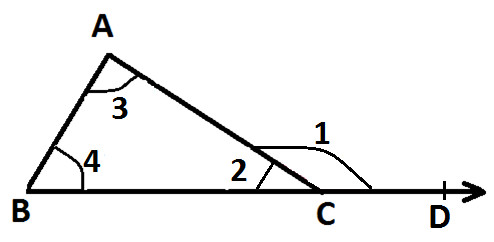
∠ 1 = External Angle
∠ 2, ∠ 3 & ∠ 4 = Interior Angles or we can also refer them as Angles of Triangle ABC
∠ 3 & ∠ 4 = Interior Opposite Angles to Exterior ∠ 1
Now, as per Angle Sum Property:
∠ 2 + ∠ 3 + ∠ 4 = 180°
Or
∠ 2 = 180° - ∠ 3 - ∠ 4 ..... (Statement 1)
And, we can see that ∠ 1 & ∠ 2 form a Linear Pair, therefore:
∠ 1 + ∠ 2 = 180°
Or
∠ 1 = 180° - ∠ 2
Put values of ∠ 2 from statement 1 and we get:
∠ 1 = 180° - (180 - ∠ 3 - ∠ 4)
Open brackets and we get:
∠ 1 = 180 - 180 + ∠ 3 + ∠ 4
Solve R.H.S and we get
∠ 1 = ∠ 3 + ∠ 4 ..... (statement 2)
Now as mentioned above:
∠ 1 = External Angle
∠ 3 & ∠ 4 = Interior Opposite Angles to Exterior ∠ 1
Put these into statement 2 and we get:
Exterior ∠ 1 = Interior Opposite ∠ 3 + Interior Opposite ∠ 4
Hence, proved:
Exterior = Sum of Interior Opposite Angles
From this property we can also conclude that:
Exterior Angle of a Triangle is Greater Than either of its Interior Opposite Angles.
Study More Solved Questions / Examples
In the following Triangle ABC, find measure of exterior ∠ 1:
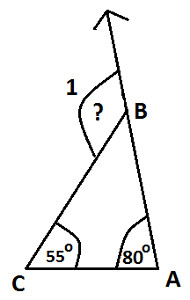 |
|
Find measure of exterior angle whose interior opposite angles are 50° & 75° |
Find error in the following diagram:
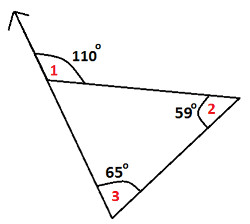
|
| | |






