|
Can two acute angles be complementary to each other ? Explain. |
Check whether the following pair of angles is complementary to each other ?
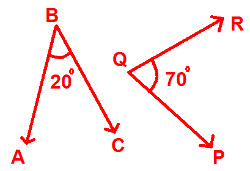
|
|
Can two obtuse angles be Complementary to each other? Explain. |
|
There are two Complementary angles; measure of one angle is 38. Find measure of other angle ? |
Are the following diagram of pair of angles Complementary to each other?
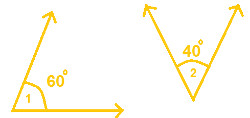 |
|
Can two right angles be Complementary to each other ? Explain. |
Study the following diagram, ∠ x = 46°, find its Complementary ∠ y.
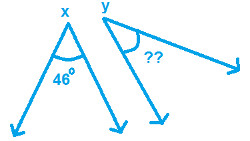 |
Check the following pair and write which are complementary angles ?
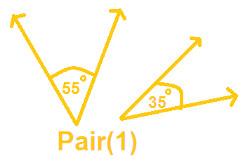
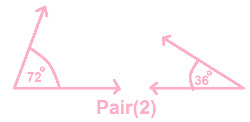
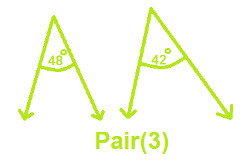
|
|
The difference in measure of two Complementary angles is 12° . Find the measures of the angles. |
|
Two angles are Complementary. Measure of one angle is twice the other. Find the measures of both the angles. |
| |






