Before you understand the property of "Equal chords are equidistant from the center of circle", you are advised to read:
What is Center of Circle ?
What are the Chords of Circle ?
What is Distance of a Line from the point ?
Observe the following diagram:
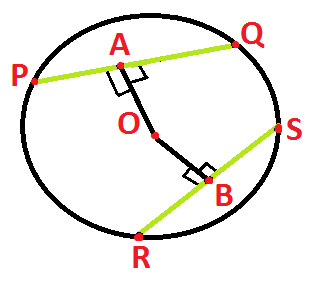
In the above diagram we have:
A circle with center O
PQ and RS are two chords of circle
PQ and RS both are equal (as highlighted in green above)
OA and OB are perpendiculars from center of circle to the chords PQ and RS respectively.
Now, observe carefully:
O is a point outside PQ and OA is perpendicular to PQ
And as per the property which says "The length of perpendicular from a point to a line is the distance of line from the point" , we get:
OA is the distance of chord PQ from center of Circle O
Similarly,
OB is a point outside RS and OB is perpendicular to RS
And as per the property which says "The length of perpendicular from a point to a line is the distance of line from the point", we get:
OB is the distance of chord RS from center of Circle O
Now, as per this property i.e. "Equal chords are equidistant from the center of circle", we get:
OA = OB
How to prove this property : Equal chords are equidistant from the center of circle
Before you prove this property of circle, you are advised to read:
What is RHS Rule of congruency in Triangles ?
What are Corresponding Parts of Congruent Triangles ?
What is Radii of Circle ?

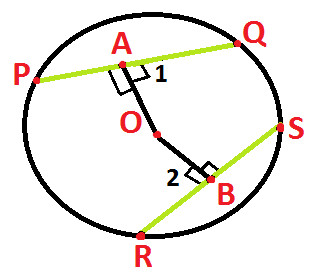
In the above diagram we have:
O is the center of the circle
PQ and RS are two equal chords of the circle (as highlighted in green above)
OA and OB are perpendiculars from center of circle to the chords PQ and RS respectively.
Since, OA is perpendicular from center O to the chords PQ and on applying the property 3 of circle "The perpendicular from the center of a circle to a chord bisects the chord" , we get:
PA = AQ
Or we can also write it as:
AQ = 1/2 of PQ ... (Statement 1)
Similarly, OB is perpendicular from center O to the chords RS and on applying the property 3 of circle "The perpendicular from the center of a circle to a chord bisects the chord" , we get:
RB = BS
Or we can also write it as:
RB = 1/2 of RS ... (Statement 2)
Now, as given in the question:
PQ = RS
Divide both side by 2 and we get:
1/2 of PQ = 1/2 of RS
Apply values from statement 1 & 2 and we get:
AQ = RB .... (statement 4)
Also, OA and OB are perpendiculars from center of circle to the chords PQ and RS respectively, so we get:
Angle 1 = Angle 2 = 90 degree each, as shown below .... (Statement 5)
Now, join points O & Q and O & R (as shown below):
This would give us two triangles i.e.
△ AOQ and △ BOR (as highlighted below):
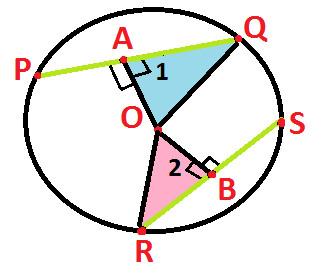
In △ AOQ and △ BOR
∠ 1 = ∠ 2 (proved in statement 5)
OQ = OR (radii of circle are always equal)
AQ = RB (proved in statement 5)
Therefore, on applying RHS Rules of congruency, we get:
△ AOQ and △ BOR
Since, we know that corresponding parts of congruent triangles are equal, so we get:
OA = OB
Hence this proves property of circle i.e. "Equal chords are equidistant from the center of circle" .
|






