| Arithmetic Additive Identity
Arithmetic Progression
Associative Property
Averages
Brackets
Closure Property
Commutative Property
Conversion of Measurement Units
Cube Root
Decimal
Distributivity of Multiplication over Addition
Divisibility Principles
Equality
Exponents
Factors
Fractions
Fundamental Operations
H.C.F / G.C.D
Integers
L.C.M
Multiples
Multiplicative Identity
Multiplicative Inverse
Numbers
Percentages
Profit and Loss
Ratio and Proportion
Simple Interest
Square Root
Unitary Method
Algebra Cartesian System
Order Relation
Polynomials
Probability
Standard Identities & their applications
Transpose
Geometry Basic Geometrical Terms
Circle
Curves
Angles
Define Line, Line Segment and Rays
Non-Collinear Points
Parallelogram
Rectangle
Rhombus
Square
Three dimensional object
Trapezium
Triangle
Quadrilateral
Trigonometry Trigonometry Ratios
Data-Handling Arithmetic Mean
Frequency Distribution Table
Graphs
Median
Mode
Range
Videos
Solved Problems
|
Home >> Decimal >> Division of Decimals >> Division of Decimal by a Whole Number (not zero) >> Division of Decimal by a Whole Number (not zero)
Before you study this concept, you are advice to study:
Define Multiples
Convert Decimal into Fraction
Convert Proper Fraction into Decimal
Place Value of Digits in Decimal
Multiplicative Inverse
Define Dividend
Define Divisor
Define Quotient
Define Remainder
You can use following two methods of Division:
Method 1: Cross Multiplication
E.g. Divide 12.5 by 5
Method 1: proceeds as
= 12.5 ÷ 5
Convert decimal into fraction and we get:
Multiply the resultant fraction with the multiplicative inverse of divisor and we get:
Solve by Cross multiplication and we get:
On solving the above expressions, we get:
Convert the fraction into decimal and we get:
= 2.5
Method 2: Long division method.
E.g. Divide 12.5 by 5 using Method 2:
Method 2 proceeds as:
= 12.5 ÷ 5
Place dividend and divisor in long division method, as shown below:
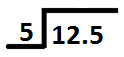
Now, we start dividing digit at tens place (1) by divisor (5).
Since 1 is less that than 5 so we take digit at tens and hundreds place and divide them together by divisor (5) i.e. 12 is to be divided by 5.
And we can see that 12 is not exactly divisible by 5, so we will choose a multiple of 5 which is nearest to 12.
And Nearest number to 12 and which is also a multiple of 5 is 10
So, Place 10 below 12 as shown below:
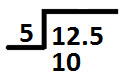
Now, 10 is a multiple of 5 and on dividing 10 by 5 we get 2.
So, we write 2 at ones place in the quotient (as shown below):
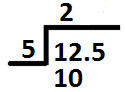
Subtract 10 from 12 and we get 2 as remainder.
Write remainder as shown below:
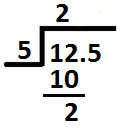
After the division of digits at tens and hundreds place there comes decimal point, so we will put decimal point in quotient too; as shown below:
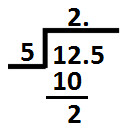
Now, place 5 (which is at tenths place in dividend) next to remainder 2 (calculated above) as shown below:
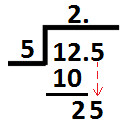
Divide 25 (shown above) by divisor 5 & we get 5
So, write 5 at tenths place in the quotient and we get:
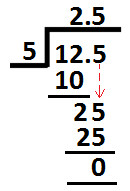
Subtract 25 from 25 (as shown above) and we get Zero as remainder.
So, this is the end of long division method and we get:
12.5 ÷ 5 = 2.5
|
|






