Diagonals of a parallelogram divide it into two congruent triangles
Before you understand this property of parallelogram, you are advised to read:
What is a Triangle ?
What are Congruent Triangles ?
What are the rules of Congruency ?
What is a Transversal Line ?
What are Pair of Alternative Interior Angles ?
Observe the following diagram:
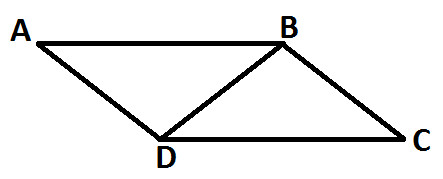
ABCD is a parallelogram
BD is a diagonal
So, as per the property, we get two equal and congruent triangles i.e.
△ ABD and △ BCD (as show in the following diagram):
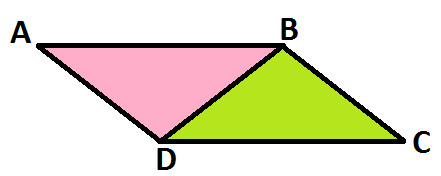
Now, let's prove the property
In order to prove this property, we have to prove that △ ABD ≅ △ BCD
Observe the following diagram:
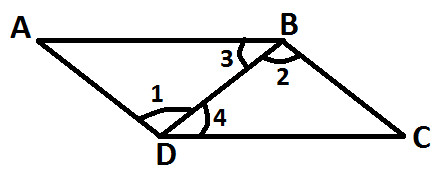
AB is parallel to CD
DB is a transversal
So pairs of alternative angles are equal and we get:
∠ 1 = ∠ 2
∠ 3 = ∠ 4
Now, In : △ ABD ≅ △ BCD
∠ 1 = ∠ 2 (proved above)
∠ 3 = ∠ 4 (proved above)
DB = BD (common line)
Hence, proved △ ABD ≅ △ BCD
|






