Congruent word means "coinciding over each other when superimposed"
Congruent object are exact copies of each other.
Congruent objects are represented with symbol: ≅
Congruence : The relation of two objects being congruent is called Congruence
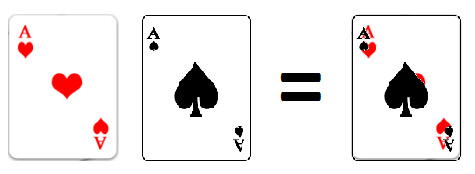
In the below figure you can see that two cards Ace of Hearts and Ace of Spades are congruent i.e. when both are placed one over other, they coincide exactly.
In the below figure you can see that two stamps are again congruent to each i.e. when both are placed one over other, they coincide exactly.

Look at the following few more congruent objects:



Let's study some more examples on congruence
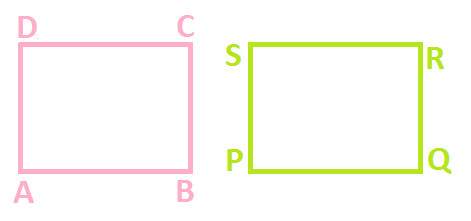
Example 1: Observe the following diagram which have two quadrilaterals ABCD and PQRS
Let's superpose PQRS on ABCD (as shown below):
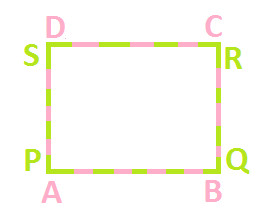
You can observe the both the quadrilateral when superpose over one another, covers each other completely. (You can try this activity with the help of tracing paper too)
Hence, we can say that Quadrilateral ABCD and PQRS are congruent.
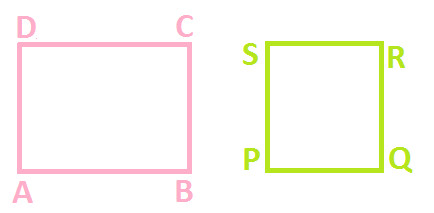
Example 2: Observe the following diagram which have two quadrilaterals ABCD and PQRS
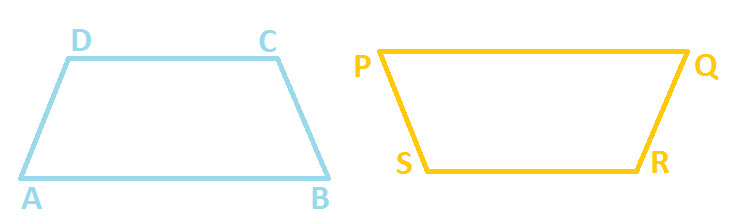
Let's superpose PQRS on ABCD (as shown below):
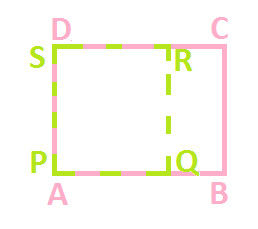
Hint: Before superpose you have to flip quadrilateral PQRS vertically.
You can observe the both the quadrilateral when superpose over one another, they covers each other completely. (You can try this activity with the help of tracing paper too)
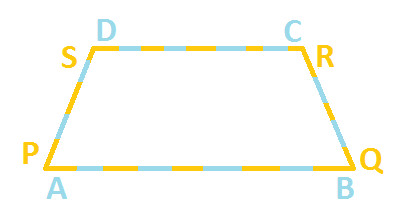
Example 3: Observe the following diagram which have two quadrilaterals ABCD and PQRS
Let's superpose PQRS on ABCD (as shown below):
You can observe the both the quadrilateral when superpose over one another, does not cover each other completely. (You can try this activity with the help of tracing paper too)
Hence, we can say that Quadrilateral ABCD and PQRS are not congruent.
Now, in example 1 and 2; figures are congruent because when you can superpose one over another, they cover each other completely.
And in example 3, figures are not congruent because when you can superpose one over another, they do not cover each other completely.
This also gives us a fact that:
Areas of Congruent Figures are always equal or we can say that congruent figures have equal areas.
But, the converse of above fact is not true i.e.:
Two figures having same areas are not always congruent
Example 4: Observe the following figures, Quadrilateral ABCD which is a rectangle and Quadrilateral PQRS which is a square
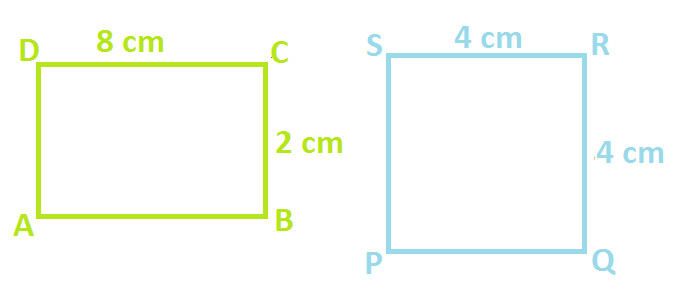
Area of rectangle ABCD = 8 X 2 = 16 cm2
Area of square PQRS = 4 X 4 = 16 cm2
You can notice that areas of both the quadrilateral are equal i.e. 16 cm2. But we cannot say that they are congruent. In order to check this, let's superpose one over another as shown below:
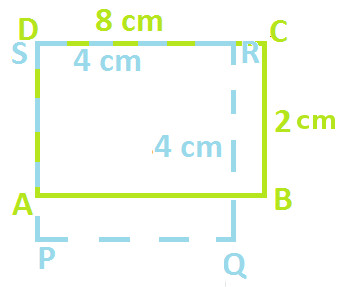
You can observe that both the figures when superpose over one another, does not cover each other completely. (You can try this activity with the help of tracing paper too)
Hence, this proves the statement that two figures having same areas are not always congruent.
|






