Before you understand the property "Chords equidistant from the center of circle are equal in length", you are advised to read:
What is Center of Circle ?
What are the Chords of Circle ?
What is Distance of a Line from the point ?
Observe the following diagram:
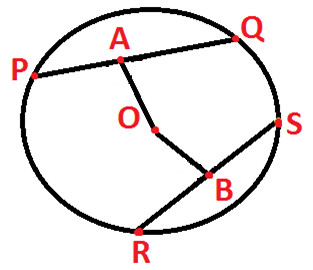
In the above diagram we have:
A circle with center O
PQ and RS are two chords of circle
OA and OB is the distance of chords PQ & RS respectively from the center of circle
OA is equal to OB
Now, as per the property 6 of circle i.e."Chords equidistant from the center of circle are equal in length", we get:
PQ = RS
How to prove this property : Chords equidistant from the center of circle are equal in length
Before you prove this property, you are advised to read:
What is RHS Rule of congruency in Triangles ?
What are Corresponding Parts of Congruent Triangles ?
What is Radii of Circle ?
What is Distance of a Line from the point ?
Property : Perpendicular from the center of a circle to a chord bisects the chord
Observe the following diagram:

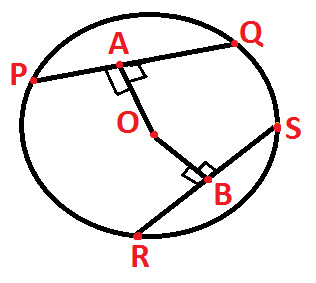
In the above diagram, we have:
A circle with center O
PQ and RS are two chords of circle
OA and OB is the distance of chords PQ & RS respectively from the center of circle
OA is equal to OB
Now, observe carefully:
Since OA and OB is the distance of chords PQ & RS respectively from the center of circle.
And as per the property which says "The length of perpendicular from a point to a line is the distance of line from the point", so we get:
OA is perpendicular to PQ and OB is perpendicular to RS (as shown below) ..... (statement 1)
Also, we know that:
O is the center of circle (given)
And OA is perpendicular to PQ (proved in above statement 1)
So apply Property 3 of circle, "The perpendicular from the center of a circle to a chord bisects the chord" and we get:
AQ = PA
Or we can write it as:
2AQ = PQ ..... (statement 2)
Similarly, O is the center of circle (given)
And OB is perpendicular to RS (proved in above statement 1)
So apply Property 3 of circle, "The perpendicular from the center of a circle to a chord bisects the chord" and we get:
RB = BS
Or we can write it as:
2RB = RS ..... (statement 3)
Now, join points O & Q and O & R (as shown below):
This would give us two triangles i.e.
△ AOQ and △ BOR (as highlighted below):
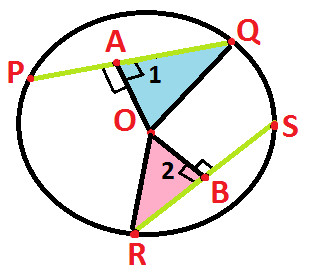
△ AOQ ^ △ BOR
Angle 1 = Angle 2 (90 degree each - proved in above statement 1)
OQ = OR (radii of circle are always equal)
OA = OB (given)
Therefore, on applying RHS Rules of congruency, we get:
△ AOQ ^ △ BOR
Since, we know that corresponding parts of congruent triangles are equal, so we get:
AQ = RB
Multiply both sides by 2 and we get:
2AQ = 2RB
Put the values from above statement 2 & 3 and we get:
PQ = RS
Hence, this proves property 6 of circle i.e. "Chords equidistant from the center of circle are equal in length"
|






