| Arithmetic Additive Identity
Arithmetic Progression
Associative Property
Averages
Brackets
Closure Property
Commutative Property
Conversion of Measurement Units
Cube Root
Decimal
Distributivity of Multiplication over Addition
Divisibility Principles
Equality
Exponents
Factors
Fractions
Fundamental Operations
H.C.F / G.C.D
Integers
L.C.M
Multiples
Multiplicative Identity
Multiplicative Inverse
Numbers
Percentages
Profit and Loss
Ratio and Proportion
Simple Interest
Square Root
Unitary Method
Algebra Cartesian System
Order Relation
Polynomials
Probability
Standard Identities & their applications
Transpose
Geometry Basic Geometrical Terms
Circle
Curves
Angles
Define Line, Line Segment and Rays
Non-Collinear Points
Parallelogram
Rectangle
Rhombus
Square
Three dimensional object
Trapezium
Triangle
Quadrilateral
Trigonometry Trigonometry Ratios
Data-Handling Arithmetic Mean
Frequency Distribution Table
Graphs
Median
Mode
Range
Videos
Solved Problems
|
Home >> Rhombus >> Area of Rhombus >> Area of Rhombus
Before you study how to calculate area of rhombus, you are advised to read:
What is Rhombus ?
How to find Area of Triangle ?
Formula to calculate Area of Rhombus:
Area of Rhombus is equals to half of the product of its diagonals
To put into mathematical formula, we get:
Area of Rhombus = 1/2 (Diagonal 1 X Diagonal 2)
Or we can it as:
Area of Rhombus = 1/2 (d1 d2)
Also, note that area of rhombus is always in square units e.g. cm2 or m2 etc .....
How formula for area of rhombus is obtained:
Observe the following Rhombus ABCD (as shown in Diagram 1)
Diagram 1:
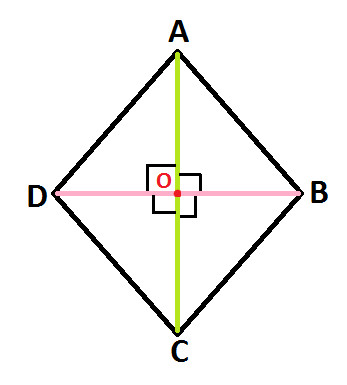
AC and DB are its diagonals
O is the point of intersection of diagonals AC and DB.
And we know that diagonals of rhombus bisect each other, so we get:
AC = AO + OC and DB = DO + OB ..... (Statement 1)
Rhombus ABCD comprises of Triangle ADB and Triangle BCD( as shown in diagram 2):
Diagram 2:
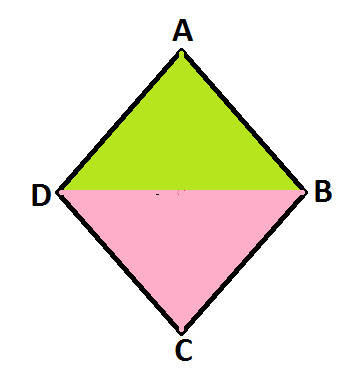 | Area of Rhombus ABCD = Area of Triangle ADB + Area of Triangle BCD ..... (Statement 2) |
|---|
Triangle ADB : Observe Triangle ADB (as shown in above diagram 1) and it has:
AO = height
DB = Base
Now apply formula of area of triangle and we get:
Area of Triangle ADB = 1/2 (Base X Height)
Area of Triangle ADB = 1/2 (DB X AO) ..... (Statement 3)
Triangle BCD : Observe Triangle BCD (as shown in above diagram 1) and it has:
OC = height
DB = Base
Now apply formula of area of triangle and we get:
Area of Triangle BCD = 1/2 (Base X Height)
Area of Triangle BCD = 1/2 (DB X OC) ..... (Statement 4)
Area of Rhombus ABCD = Area of Triangle ADB + Area of Triangle BCD
Area of Rhombus ABCD = 1/2 (DB X AO) + 1/2 (DB X OC)
Take 1/2 DB common and we get:
= 1/2 DB (AO + OC)
As mentioned above in statement 1 (AO + OC = AC), so we get:
= 1/2 DB X AC
Since DB and AC are diagonals of Rhombus ABCD, so we get:
= 1/2 X Diagonal 1 X Diagonal 2
Or we can write it as:
= 1/2 X d1 X d2
Hence in this way formula for area of rhombus is obtained:
Area of Rhombus = 1/2 (d1 d2)
Let's use the formula to solve following example:
Example: Find area of Rhombus whose diagonals are 8 cm and 10 cm ?
Solution: As per the given question:
Diagonal 1 = 8 cm
Diagonal 2 = 10 cm
Apply formula for area of Rhombus:
Area of Rhombus = 1/2 (d1 d2)
Put given values of both the diagonals and we get:
= 1/2 (10 X 8)
= 1/2 X 80
= 40
Area of Rhombus = 40 cm2
|
|






