Below figure represent Bisector of angle with the help of Compass.
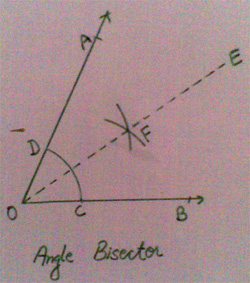
In the above diagram, given angle AOB is to be bisected with the help of compass, in the following steps.
1). Given Angle AOB is to be bisected.
2). With O as centre and any convenient radius draw an arc,
which cuts OB at C and and OA at D.
3). With C as centre and any convenient radius, draw an arc
4). With D as centre and same radius (as of step 3) draw another arc, which cuts previous arc F.
5). Join OF and extend upto E.
6). EO is the bisector of Angle AOB.
Therefore, Angle AOE = Angle BOE.
|






